面试这种场合,大家都懂,面试官总喜欢出点“奇奇怪怪”的题目,问你点“看似不可能”的问题——比如:
40亿个QQ号要去重,内存还只能给你1GB。
就像老板让你用两块钱预算搞个全公司团建,还得拍成《向往的生活》那种高级感。
这不,最近就有小伙伴再面试过程中遇到这道看似不可能,实则还是能搞定的面试题。
1. 数据规模分析
- 数据量:题目中的40亿个QQ号意味着你需要处理的数据集非常庞大。如果每个QQ号以整数形式存储(比如32位整数),每个QQ号占用4字节空间。
- 总内存需求:如果直接将这40亿个QQ号存入内存中,所需空间为:
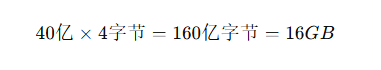
这个规模远超1GB内存的限制,因此直接在内存中存储所有QQ号是不可能的。
2. 内存限制分析
- 1GB内存限制:题目要求只能使用1GB的内存,这意味着你需要使用非常高效的算法和数据结构来存储和处理这40亿个QQ号,尤其是在去重的过程中。
最近无意间获得一份阿里大佬写的刷题笔记,一下子打通了我的任督二脉,进大厂原来没那么难。这是大佬写的,7701页的BAT大佬写的刷题笔记,让我offer拿到手软
1. 什么是BitMap?它有什么用?
BitMap,顾名思义,就是用“位”来存储数据的技术。我们平时可能听过“字节”、“兆字节”这些词,但BitMap更小巧精悍,直接用最小的数据单位——“位”——来操作。在计算机里,1个字节(Byte)等于8位(bit),也就是说,一个字节能记录8个信息点。这个小小的技巧让BitMap在处理海量数据的时候非常高效。
举个简单的例子,我们生活中常常要做记录,比如每天上班打卡。
如果你每天只打一次卡,我们可以用一张纸每天划一个“√”来表示今天打了卡。

这就是最简单的“位图”概念——每一天的卡记录其实可以只占一个“位”大小的信息。
类似的,BitMap在计算机里是用“位”来表示某个数据是否存在。打个比方,如果你有40亿个QQ号,你不需要为每个QQ号都分配一个独立的空间(比如字符串),而是通过一个位图,按顺序标记“这个号有没有出现过”。它的核心优势就是省内存,因为一个bit只占用一个二进制位,这对海量数据来说节省了很多空间。
2. 如何使用BitMap进行40亿个QQ号去重?
假设你现在有40亿个QQ号需要去重。如果每个QQ号都是一个32位的整数,那如果直接存储这些QQ号,将占用16GB内存(40亿个QQ号 × 每个号4字节)。但我们假设QQ号的最大范围也就是从1到40亿,意味着我们最多需要存储40亿个数的“有”或“没有”状态,用BitMap刚好可以应对。
具体步骤如下:
第一步:初始化位图
我们需要一个大小足够的位图来记录这40亿个QQ号。既然1个bit能表示一个QQ号有没有出现,那40亿个QQ号就需要40亿个bit。这样一个位图大概需要500MB的内存(40亿bit / 8 = 500MB),这和我们要处理的1GB内存限制相符。
第二步:读取QQ号并标记位图
你可以想象一下这个位图是一张巨大的“表”,上面有40亿个小格子,每个小格子代表一个QQ号的位置,初始时每个格子都是“0”,表示这个号码还没出现。当我们逐个读取QQ号时,假设读到第一个QQ号是,那我们就把位图中的第个位置标记为“1”,表示这个QQ号出现了。重复的号码再次被读取时,它对应的位已经是“1”了,所以我们就知道这个QQ号已经存在,不会重复处理。
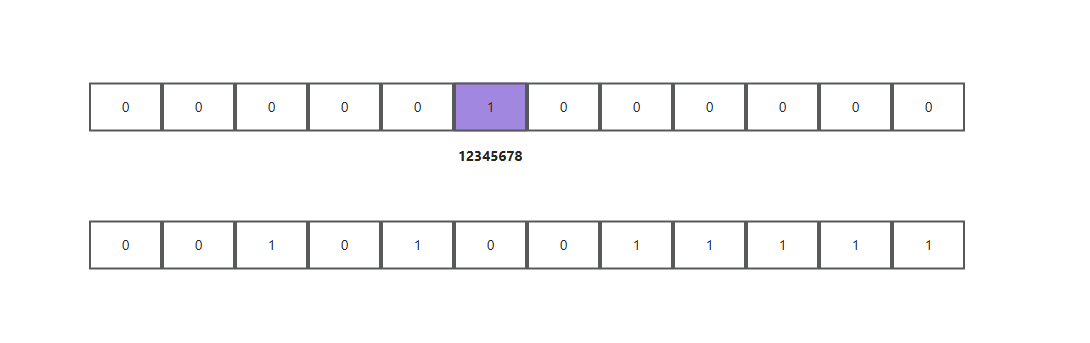
第三步:扫描位图得到去重结果
当所有QQ号都处理完之后,去重的过程就完成了。接下来,我们只需要遍历这个位图,找到所有标记为“1”的位,就可以得到所有去重后的QQ号。
这个过程简单来说就是:
- 初始化一个40亿个格子的表,开始时所有格子都是“0”;
- 每次读取一个QQ号,就标记它对应的格子为“1”;
- 读完所有QQ号后,找到所有格子里是“1”的,输出这些位置的号码,就完成了去重。
3. BitMap位图的优势和不足
优势
1. 节省内存
BitMap的最大优势就是节省内存。假设每个QQ号需要4字节的空间,而用BitMap的方式,一个QQ号只需要1个bit,也就是1/32的内存消耗。对于40亿个QQ号来说,这个节省的效果非常显著。在我们的例子里,原本需要16GB的内存,而BitMap只用了500MB左右,就完成了同样的任务。
2. 高效处理海量数据
当数据量非常大时,传统的去重方法可能会让计算机内存“吃不消”,直接“宕机”或者速度变得极慢。而BitMap通过将大量数据压缩成极小的空间,使得处理海量数据时既不拖慢系统,也不会用完内存。在内存受限的场景中,它是非常实用的工具。
举个职场例子:就像你要组织一次全公司活动,需要统计上千名员工的参与情况。如果你每个人都开一个文件来记录信息,文件可能会堆成山。而如果你只需要在一张表上用一个小勾表示“是否参加”,这就是BitMap的做法——用最少的资源解决问题。
3. 时间复杂度低
在用BitMap去重时,标记和查询某个QQ号是否出现过的操作都可以在常数时间内完成。也就是说,处理每个QQ号的时间不会随着数据量增多而变长,这一点对于处理海量数据尤其重要。
不足
1. 适用场景有限
BitMap虽然节省内存,但它只能用来处理“整数”类的数据。如果我们处理的不是QQ号,而是其他需要更复杂数据结构的内容,比如字符串(例如邮箱地址),BitMap就不适用了。它擅长的是处理像QQ号这种可以直接映射到位图上、并且取值范围明确的数据。
打个比方,如果我们公司里有很多部门,每个部门的员工人数不一样,而且我们要分别统计他们的参与活动情况,BitMap的做法就显得有些局限性。它不能灵活处理更复杂的、多层次的结构化信息。
2. 存储“稀疏”数据时效率不高
如果QQ号的分布很稀疏,比如说,我们有40亿的号码范围,但实际出现的QQ号只有几百万,这时候大部分位图格子都是空的,浪费了很多空间。换句话说,BitMap的效率依赖于数据的密集度。如果QQ号分布得很松散,可能会占用比实际数据多得多的内存。
3. 位图最大值限制
BitMap的大小必须提前确定。如果我们处理的QQ号超过了原先设置的最大值(比如说你预期最多处理40亿个号码,但突然遇到了超过40亿的QQ号),那么位图就“装不下”了,需要重新扩展空间,而这个操作可能会非常繁琐和耗时。举个日常
例子,如果你预定了一个500人的会议场地,结果当天来了600人,这时你得临时找更大的场地,增加座位。对于BitMap来说,预设好最大范围是非常重要的,一旦溢出,整个系统就可能需要大规模调整。
最近无意间获得一份阿里大佬写的刷题笔记,一下子打通了我的任督二脉,进大厂原来没那么难。这是大佬写的,7701页的BAT大佬写的刷题笔记,让我offer拿到手软
1. 什么是布隆过滤器?实现原理是什么?
布隆过滤器,听起来像是一种很高深的技术,其实它的原理非常简单,主要用来快速判断某个元素是不是已经存在过。
它特别适合处理海量数据,但不同于普通的集合或者列表,布隆过滤器的最大特点是节省空间,也就是说,在存储大量数据时,它几乎不怎么占用内存。
为了让这个概念更加清晰,咱们来打个比方:
假设你是公司的HR,负责一个超大的应聘者名单。名单上有上百万个名字,你每天都要检查一个名字是否已经在这个名单里。正常情况下,你需要一个非常庞大的数据库或者Excel表格,才能够存储这些名字,并进行查找,但布隆过滤器的好处是,它通过**“牺牲一点点准确性”来换取极大的存储空间和速度优势。**
也就是说,它能够快速告诉你:“这个名字可能已经在名单里了”,但有一点点可能性它会误判。
实现原理
布隆过滤器的核心原理就是使用多个哈希函数。
每次我们插入一个元素(比如一个QQ号或一个名字),布隆过滤器会通过几个哈希函数,生成几个不同的位置,把这些位置的“位”(bit)设置为1。之后,当你需要检查某个元素是否已经存在时,它会用同样的哈希函数去检查对应位置的位是否都已经是1。如果都是1,那么它会告诉你:“这个元素可能存在过”。如果有任何一个位是0,它就可以非常肯定地告诉你:“这个元素绝对没出现过”。
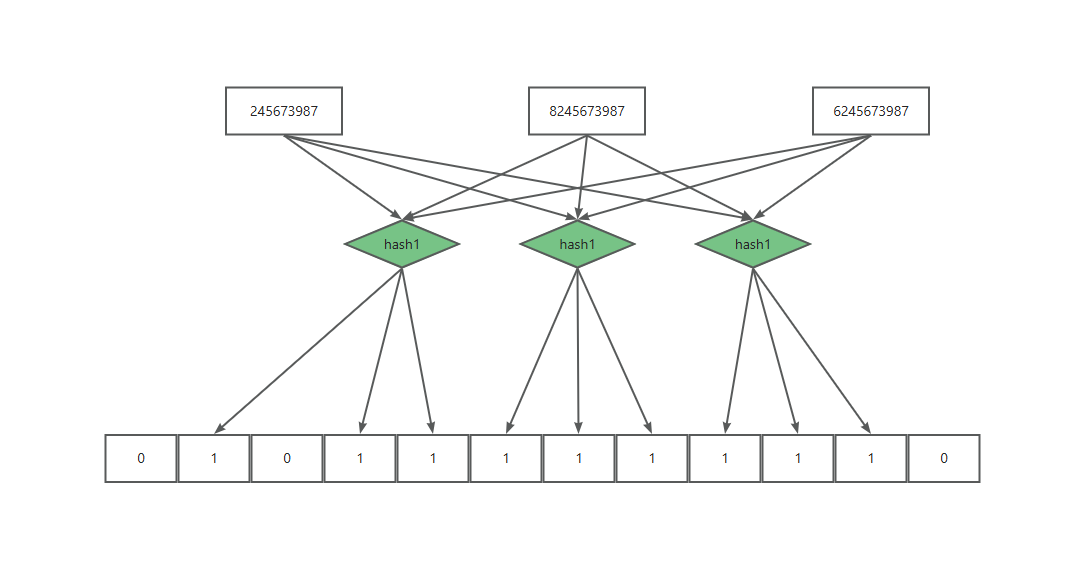
2. 什么是哈希冲突?
说到布隆过滤器,就不得不提到哈希函数,而哈希函数容易引发的一个问题就是“哈希冲突”。
简单来说,哈希函数的作用是将任意大小的数据转化成固定长度的值。
比如,你可以用一个哈希函数将一串名字“张三”转换为一个固定长度的数字或字符。问题是,如果两个不同的元素,比如“张三”和“李四”,经过同样的哈希函数转换后,结果是相同的,那就发生了哈希冲突。
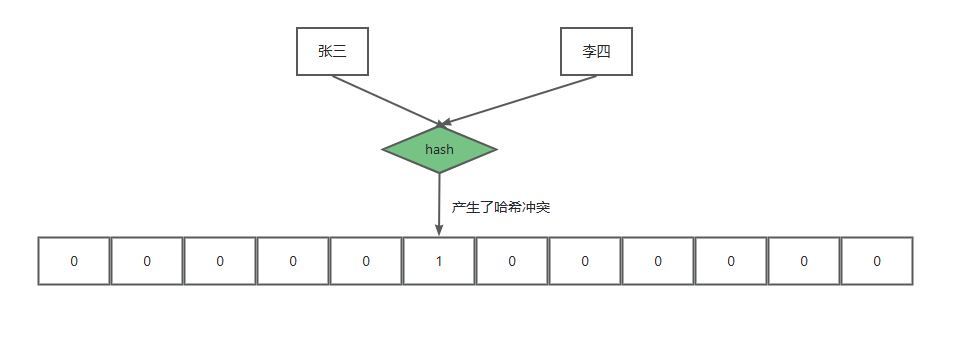
这有点像公司里有两个员工同名同姓,两个“张伟”都被安排在同一个工位上,这显然会带来混乱。哈希冲突虽然不多见,但在处理大规模数据时是不可避免的。布隆过滤器通过使用多个哈希函数,大大减少了冲突的可能性,因为每个元素都要通过多个哈希函数生成多个位置,这样可以避免因为单个哈希冲突带来的误判。
3. 布隆过滤器的工作过程
布隆过滤器的工作过程其实很简单,核心步骤有两个:添加数据和查询数据。
添加数据
-
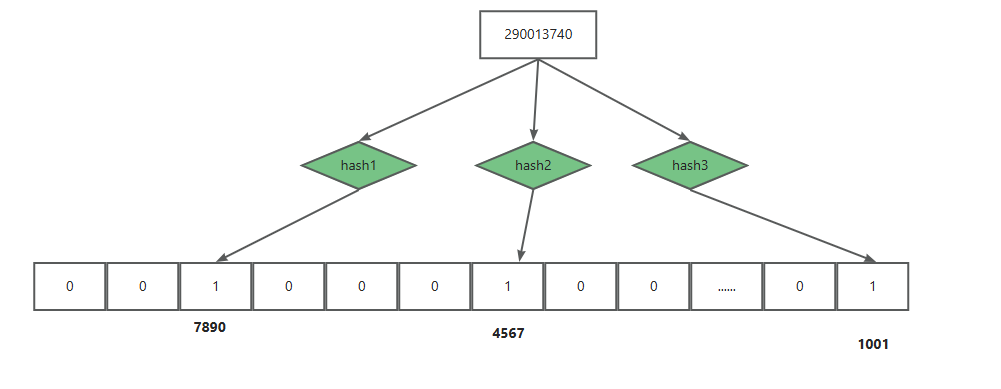
当你往布隆过滤器里添加一个新元素时,比如一个QQ号,布隆过滤器会通过多个哈希函数生成几个位置。假设有三个哈希函数,分别生成了位置、和。
-
布隆过滤器就会在这三个位置上把对应的“位”设为1。
-
重复这个过程,对于每一个新的元素,它都会通过哈希函数找到多个位置,并把这些位置的位都设置为1。
查询数据
-
当你查询某个QQ号是否存在时,布隆过滤器会用相同的哈希函数生成位置,比如你查询的QQ号生成了位置、和。
-
然后,布隆过滤器检查这几个位置的位是否都是1。如果都是1,那么它会告诉你:“这个QQ号可能已经存在”。如果有任何一个位是0,它会告诉你:“这个QQ号肯定不存在”。
注意,这里有个“可能”的说法。因为布隆过滤器有一定的误判率——它可能会错误地告诉你某个元素存在,但它不会错判不存在的情况。换句话说,布隆过滤器可以提供“假阳性”,但绝对不会给出“假阴性”。
4. 布隆过滤器的应用场景
布隆过滤器非常适合处理那些需要快速判断存在性的问题,尤其在数据量巨大但又对误判要求不高的情况下。以下是一些常见的应用场景:
1. 数据库缓存
假设你正在处理一个电商系统,数据库里有上百万个商品。每次用户查询商品时,你得先去数据库查一遍。如果商品不存在,那你就白费力气了。
这时,你可以在数据库之前加一个布隆过滤器,先用它来判断商品是否存在。如果布隆过滤器说“商品不存在”,那你就不用去查数据库了;如果布隆过滤器说“可能存在”,你再去查数据库,这样能节省大量查询时间。
这个也是解决缓存穿透的一个方案
2. 网络防火墙
布隆过滤器还能用于网络防火墙,比如判断一个IP地址是否是已知的攻击者IP。如果你有一个巨大的黑名单,用布隆过滤器可以快速判断某个IP是否有问题,而不需要查完整的黑名单列表。
3. 爬虫去重
当你写一个网络爬虫时,你不希望爬虫重复抓取已经抓取过的页面。这时候,你可以用布隆过滤器来记录已经抓取过的页面URL,避免重复工作。
4. 垃圾邮件过滤
邮箱系统可以用布隆过滤器来快速判断某封邮件是否是垃圾邮件。布隆过滤器可以通过多个哈希函数快速检测出已知的垃圾邮件模式,从而提高处理效率。
5. 如何实现布隆过滤器?(使用Redission版本举例)
Redission是一个在Java中非常常见的工具库,它可以轻松集成Redis,并且支持布隆过滤器功能。我们可以利用Redission提供的API,快速实现布隆过滤器。下面是如何用Redission实现一个简单的布隆过滤器的过程。
第一步:导入依赖
首先,确保你的项目中引入了Redisson的依赖。以下是Maven的配置:
第二步:初始化Redisson客户端
接下来,你需要初始化Redisson客户端,并连接到Redis服务器:
这段代码会连接到本地的Redis服务器。如果你的Redis服务器在其他地址,替换即可。
第三步:创建布隆过滤器
创建布隆过滤器时,我们需要指定元素数量和误判率。例如,假设你预计要处理100万个元素,误判率希望控制在0.01%:
这段代码初始化了一个布隆过滤器,预计容纳100万个元素,误判率是0.1%。
第四步:添加和查询数据
接下来,往布隆过滤器中添加数据和查询数据。
这段代码展示了如何往布隆过滤器中添加QQ号,以及如何判断某个QQ号是否已经存在。
第五步:关闭连接
操作完成后,记得关闭Redisson客户端:
选择建议:
- 如果需要灵活性较高、且愿意为优化误判率而进行一些复杂操作,可以选择布隆过滤器。
- 如果你追求简单、直接、无误判的解决方案,选择位图。
总结:
选择布隆过滤器:
- 数据量非常大(数百万甚至数亿条);
- 允许少量误判(假阳性);
- 内存有限且需要高效存储;
- 数据类型多样,可能是字符串、URL等非整数型数据;
- 数据规模不固定,或者数据分布比较稀疏。
选择位图(BitMap):
- 数据为整数型,且取值范围明确;
- 数据量大且分布较为密集;
- 不能容忍任何误判(需要100%准确性);
- 内存空间充足,可以根据数据范围分配足够的位图大小。
最后说一句(求关注,求赞,别白嫖我)
最近无意间获得一份阿里大佬写的刷题笔记,一下子打通了我的任督二脉,进大厂原来没那么难。
这是大佬写的, 7701页的BAT大佬写的刷题笔记,让我offer拿到手软
本文,已收录于,我的技术网站 cxykk.com:程序员编程资料站,有大厂完整面经,工作技术,架构师成长之路,等经验分享
求一键三连:点赞、分享、收藏
点赞对我真的非常重要!在线求赞,加个关注我会非常感激!
本文地址:http://lanlanwork.gawce.com/quote/7001.html 阁恬下 http://lanlanwork.gawce.com/ , 查看更多

